|
5.4.
Функциональный ЦАП с линейным преобразованием
управляющего кода
Второй
способ, использующий степенную
аппроксимацию, заключается в
следующем. На рассматриваемом отрезке
[a,
b]
функция f(x)
заменяется многочленом
Pn(x)=
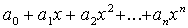 .
.
Моделирование
многочлена осуществляется
каскадно соединенными ЦАП (рис. 5.18).
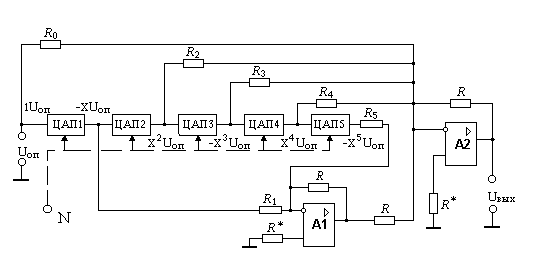
В
качестве ЦАП, изображенных на схеме,
применяют умножающие ЦАП, которые
могут работать с двухполярным опорным
напряжением. Выходное напряжение
таких ЦАП определяется по формуле:
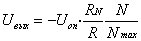 ,
,
где
N
- текущий цифровой код, который
изменяется в пределах от 0 до Nmax-1;
Nmax=2m,
m
- разрядность ЦАП; R
- сопротивление матрицы резисторов; RN
- сопротивление резистора в цепи
обратной связи ОУ ЦАП; Uоп
- опорное
напряжение.
Отношение
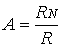 называют
масштабным коэффициентом или
масштабным множителем. Его можно
называют
масштабным коэффициентом или
масштабным множителем. Его можно
изменять в широких пределах, изменяя RN.
В
схеме, приведенной на рис. 5.18, при
подаче на цифровые входы ЦАП кода N,
на выходе 1-го ЦАП формируется
напряжение, равное:
U1=-
UопA
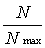 .
.
Это
напряжение является входным для 2-го
ЦАП, а напряжение на его выходе будет
определяться соотношением:
U2=- U1A
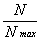 =Uоп(- А
=Uоп(- А
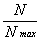 )2.
)2.
Продолжая
этот ряд, для k-го
ЦАП можно записать:
Uk
=
Uоп(- А
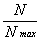 )k.
)k.
Напряжения
с выходов ЦАП через резисторы R1, R2, ..., R5
подаются на вход сумматора А2. Для обеспечения необходимого
знака, напряжения с выходов первого и
пятого ЦАП проходят через инвертор А1. Дополнительно на сумматор через
резистор R0 подается
опорное напряжение. На выходе
сумматора формируется напряжение Uвых:
Uвых=-
(
 );
);
или,
с учетом предыдущего уравнения:
Uвых=-
Uоп
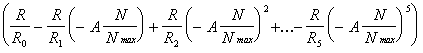 .
.
Если
обозначить
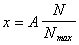 ,
,
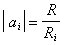 , то последнее уравнение примет вид:
, то последнее уравнение примет вид:
Uвых=-
Uоп(a0+a1x+a2x2+а3х3+а4х4+a5 x5)» - Uоп f(x).
Коэффициенты
многочлена, реализуемого данной
схемой, имеют следующие знаки: а0>0, а1>0, а2>0, а3<0,
а4>0, а5>0. Если
коэффициенты имеют другие знаки, то
схема претерпевает лишь
незначительные изменения. Таким
образом, мы получаем выходное
напряжение пропорциональное
аппроксимируемой функции f(x).
Необходимо
указать на ограничение, которое
накладывается каскадным включением
ЦАП на диапазон изменения масштабного
коэффициента А.
При подаче на цепочку ЦАП кода,
близкого к Nmax,
выходное напряжение k-го
ЦАП пропорционально Uоп(-
A)k.
Для А>1
эта величина возрастает по
геометрической прогрессии и может
приводить к насыщению операционных
усилителей. Поэтому выгодно
устанавливать А
равным 1 и аппроксимировать функцию исходя
из того, что аргумент х
изменяется от 0 до 1.
Из
вышесказанного следует, что для
воспроизведения многочлена Pn(x)
степени n
необходимо n
каскадно
включенных ЦАП. Коэффициенты
многочлена реализуются подбором
резисторов R,
R0 ,R1, ... Rk,
а знаки слагаемых устанавливаются при
помощи инвертора.
Для
того чтобы погрешность, вызванная
аппроксимацией (методическая
погрешность), была минимальна,
необходимо соответствующим образом
подобрать коэффициенты многочлена.
Рассмотрены
три метода вычисления этих
коэффициентов.
Наиболее
распространенный метод аппроксимации
функции f(x)
– ее
разложение в ряд Тейлора. В общем виде
это разложение функции f(x)
в
окрестности точки х0
осуществляется по формуле:
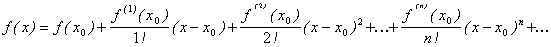 .
.
Разложение
функции в ряд Тейлора не является
единственным. Существует возможность
разложить функцию в ряд по обобщенным
многочленам, например, по многочленам
Лежандра, Чебышева, Якоби, Эрмита или
Лагерра. Здесь мы остановимся на
многочленах Чебышева, поскольку они
дают наилучшее приближение.
Для
нахождения коэффициентов Ck
разложения по многочленам Чебышева
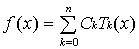 используем
следующие формулы:
используем
следующие формулы:
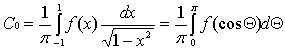 ,
,
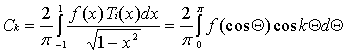 , k
> 0.
, k
> 0.
Подставляя
вместо степеней х
их выражения через многочлены
Чебышева, а затем, приводя подобные
члены при многочленах одной степени,
получим искомый многочлен Pn(x)=
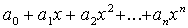 .
.
Оценить
погрешность, даваемую разложением
функции f(x)
в ряд по многочленам Чебышева в общем
виде, очень трудно. Но согласно общим
теоремам теории аппроксимации это
разложение дает наилучшее
приближение из всех возможных.
Необходимо также отметить, что
разложение функции f(x)
по
многочленам Чебышева возможно только
для функций, имеющих непрерывную
первую производную на отрезке [-1, 1].
Это условие обеспечивает сходимость
ряда к функции f(x).
Для всех простейших функций это
условие выполняется.
Следующий
метод основан на теории интерполяции.
В этом случае строят многочлен, который в n+1
заданных точках х0,
х1, . . . xn,
принимает значения f(x0), f(x1), . . . f(xn),
а в
остальных точках отрезка
[a,
b], принадлежащего области определения
f(x),
приближенно представляет функцию f(x)
с той или
иной степенью точности. Для
нахождения коэффициентов многочлена ak
составляется
система уравнений:
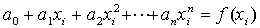 , ( i
= 0, 1, 2, . . . , n
),
, ( i
= 0, 1, 2, . . . , n
),
которая
легко решается, например, методом
Крамера.
Пример.
Калибратор
фазы с линейным преобразованием
управляющего
кода в фазовый сдвиг
Широкое
распространение получают калибраторы
фазы, принцип действия которых
заключается в суммировании двух
синусоидальных напряжений, сдвинутых
одно относительно другого на 90°.
Диапазон регулирования фазового
сдвига при этом составляет 0-90°,
а его расширение до 360°
осуществляется введением коммутатора
опорных напряжений.
При
регулировании фазового сдвига в
пределах 0-90°
выходное напряжение калибратора фазы
формируется в соответствии с
зависимостью
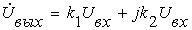 ,
(*)
,
(*)
где
Uвх -
амплитуда опорных напряжений;
k1 и
k2 - весовые коэффициенты.
Амплитуда
и фаза выходного напряжения связаны с
весовыми коэффициентами k1 и k2
соотношениями
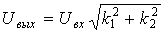 ;
;
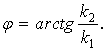
Калибраторы
фазы, управляемые цифровым кодом,
должны обеспечивать линейное
преобразование управляющего кода в
фазовый сдвиг выходного напряжения.
Кроме того, в большинстве
практических случаев необходимо
обеспечить постоянство амплитуды
выходного напряжения во всем
диапазоне регулирования фазового
сдвига. Для выполнения этих
требований весовые коэффициенты k1 и k2
должны быть связаны с управляющим
кодом нелинейными зависимостями.
В
калибраторе фазы, структурная схема
которого представлена на рис.5.19,
выходное напряжение является суммой
двух синусоидальных напряжений
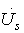 и
и
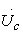 , сдвинутых
одно относительно другого на 90°.
Они формируются из входного
синусоидального напряжения
, сдвинутых
одно относительно другого на 90°.
Они формируются из входного
синусоидального напряжения
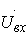 цепью
каскадно включенных цифроаналоговых
преобразователей ЦАП1 - ЦАП7 и
инвертирующими сумматорами А1 - А4.
цепью
каскадно включенных цифроаналоговых
преобразователей ЦАП1 - ЦАП7 и
инвертирующими сумматорами А1 - А4.
Передаточная
функция i-го ЦАП
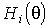 выражается
линейной зависимостью
выражается
линейной зависимостью
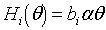 ,
,
где
bi -
масштаб преобразования i-го
ЦАП;
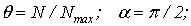
N
и
Nmax -
текущее и максимальное значения
управляющего кода.
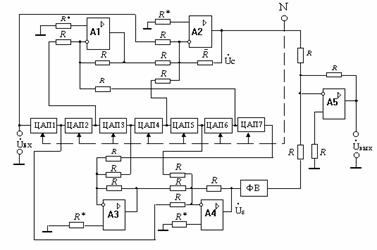
Рис.
5.19. Калибратор фазы с линейным
преобразованием управляющего
кода
в фазовый сдвиг
Применяемые
в калибраторе фазы ЦАП имеют малое
выходное сопротивление, что допускает
их каскадное включение без нарушения
нормального режима работы каждого
отдельно взятого ЦАП. Поэтому
передаточную функцию n
каскадно включенных ЦАП с достаточной
степенью точности можно записать в
виде
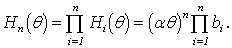
На
вход первого ЦАП, являющегося входом
калибратора фазы, с внешнего
генератора поступает синусоидальное
напряжение
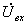 . Из него цепью каскадно включенных
ЦАП формируются напряжения, амплитуды
Un которых
связаны с управляющим кодом
соотношением
. Из него цепью каскадно включенных
ЦАП формируются напряжения, амплитуды
Un которых
связаны с управляющим кодом
соотношением
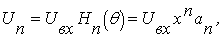
где
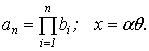
Напряжения
 с выходов ЦАП
и входное напряжение используются для
формирования двух синфазных
напряжений
с выходов ЦАП
и входное напряжение используются для
формирования двух синфазных
напряжений
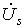 и
и
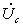 , причем напряжение
, причем напряжение
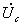 формируется
из входного напряжения и напряжений с
выходов ЦАП с четными номерами, а
выходные напряжения нечетных ЦАП
используются для формирования
напряжения
формируется
из входного напряжения и напряжений с
выходов ЦАП с четными номерами, а
выходные напряжения нечетных ЦАП
используются для формирования
напряжения
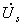 . Полагая весовые коэффициенты
суммируемых напряжений
. Полагая весовые коэффициенты
суммируемых напряжений
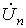 и
и
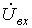 равными
единице и учитывая дополнительное
инвертирование соответствующих
напряжений сумматорами А1
и А3,
зависимости амплитуды напряжений
равными
единице и учитывая дополнительное
инвертирование соответствующих
напряжений сумматорами А1
и А3,
зависимости амплитуды напряжений
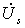 и
и
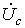 от
управляющего кода в соответствии с (4.5)
можно представить в виде
от
управляющего кода в соответствии с (4.5)
можно представить в виде
Us
=
-
Uвх(a1x-
a3x3+a5x5-
a7x7) = Uвхk2;
Uc
=
-
Uвх(1-
a2x2+a4x4-
a6x6) = Uвхk1.
Таким
образом, амплитуды напряжений
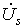 и
и
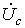 связаны с
амплитудой синусоидального
напряжения
связаны с
амплитудой синусоидального
напряжения
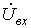 , поступающего на вход калибратора
фазы, коэффициентами k1
и k2, которые в свою очередь имеют
нелинейную зависимость от
управляющего кода.
, поступающего на вход калибратора
фазы, коэффициентами k1
и k2, которые в свою очередь имеют
нелинейную зависимость от
управляющего кода.
k1
= 1-
a2x2+a4x4-
a6x6;
k2
= a1x-
a3x3+a5x5-
a7x7.
Чтобы
получить фазовый сдвиг 90°
между напряжениями
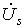 и
и
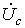 , одно из них,
, одно из них,
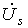 , подается на вход фазовращателя ФВ, в
результате чего на входы сумматора А5
поступают напряжения Uc
и jUs.
Выходное напряжение сумматора А5,
являющееся выходным напряжением
калибратора фазы, описывается
соотношением (*).
, подается на вход фазовращателя ФВ, в
результате чего на входы сумматора А5
поступают напряжения Uc
и jUs.
Выходное напряжение сумматора А5,
являющееся выходным напряжением
калибратора фазы, описывается
соотношением (*).
Фаза
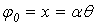 определяется
управляющим кодом, а амплитуда
выходного напряжения зависит только
от амплитуды входного напряжения Uвх
(в рассмотренном случае Uвых=Uвх).
определяется
управляющим кодом, а амплитуда
выходного напряжения зависит только
от амплитуды входного напряжения Uвх
(в рассмотренном случае Uвых=Uвх).
Разность
между расчетными и заданными
значениями фазы и амплитуды выходного
напряжения будет тем меньше, чем
точнее моделируются функциональные
зависимости cosx и sinx.
Функции
cosx и sinx могут
быть представлены в виде суммы
степенного ряда, причем тем точнее,
чем больше членов степенного ряда при
этом используется и чем меньше
диапазон изменения аргумента x.
Когда заданы число членов ряда и
диапазон изменения переменной x,
задача минимизации погрешности
моделирования сводится к точному
вычислению коэффициентов при
суммирующихся членах ряда.
В
табл. 5.5 приведены значения
коэффициентов an,
рассчитанные для трех случаев, когда
высшая степень x и число ЦАП в схеме калибратора фазы
соответственно равны семи, шести и
пяти.
Методическая
фазовая погрешность и нестабильность
амплитуды выходного напряжения
определяются соотношениями
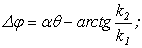
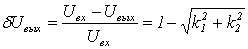 .
.
Графики
этих зависимостей приведены на рис. 5.20
(а, б) (где m -
число ЦАП в схеме), а их максимальные
значения указаны в табл. 5.5.
Таблица
5.5.
|
Коэффициенты
an
|
d
Uвых,
%
|
D
j,
°
|
|
a1
= 1,000
a2 = 0,4999
a3
= 0,1666
a4 = 0,0416
a5
= 0,0083
a6 = 0,0013
a7
= 0,0002
|
0,005
|
0,003
|
|
a1
= 1,000
a2 = 0,4999
a3
= 0,1661
a4 = 0,0416
a5
= 0,0076
a6 = 0,0013
|
0,016
|
0,005
|
|
a1
= 1,000
a2 = 0,4967
a3
= 0,16605
a4 = 0,03705
a5
= 0,00761
|
0,06
|
0,06
|
|
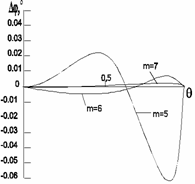
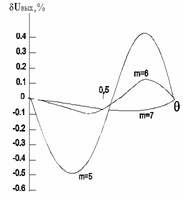
Рис.
5.20. Зависимости погрешности
фазового сдвига Dj
(а) и модуля dUвых
напряжения выхода (б)
|
Анализ
полученных результатов показывает,
что уже при использовании шести ЦАП
можно построить калибратор фазы с
высокими метрологическими
характеристиками. Погрешность
калибратора фазы в основном будет
определяться погрешностью настройки
ЦАП на заданный масштаб
преобразования, паразитными фазовыми
сдвигами в ЦАП и сумматорах на высоких
частотах, точностью поддержания
фазового сдвига 90°.
Экспериментальная
проверка макета калибратора фазы
показала, что в диапазоне 30 Гц - 20 кГц
основная погрешность не превышает 0,1°
и достигает максимального значения на
верхней частоте указанного диапазона
(испытания макета проводили с
использованием калибратора фазы,
прошедшего метрологическую
аттестацию во ВНИИМ).
|