|
2.10.
Анализ комбинационных устройств
Анализ - это процесс получения
логического выражения для
существующего комбинационного
устройства, т.е.
при анализе необходимо получить
оптимальное логическое выражение (если
требуется и СНДФ) имеющейся
логической схемы.
Необходимость
в анализе КУ возникает при
модернизации логических устройств,
обновлении элементной базы, а также
при оптимизации схемы цифрового
автомата.
Рассмотрим
пример анализа простейшего
логического устройства. Пусть дан
фрагмент схемы комбинационного
устройства, приведенный на рис. 2.31.
Требуется минимизировать логическое
выражение, реализуемое этой схемой и
синтезировать новую схему в базисе “И-НЕ”.
В
начале анализа присваиваем имена
промежуточным функциям на выходе
каждого элемента и запишем логические
выражения для этих функций
Z1
=
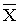 1; Z2
=
1; Z2
=
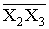 ; Z3
= Z1
+ Z2
=
; Z3
= Z1
+ Z2
=
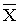 1 +
1 +
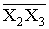 ;
;
Z4
= Z3
X1
= (
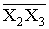 )X1
+ X1
)X1
+ X1
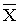 1 = X1
1 = X1
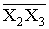 .
.
Выходная функция КУ представляет
дизъюнкцию трех переменных (функций Z2,
Z4 и Х4) с последующей
инверсией
Y =
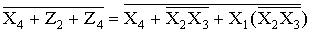 .
.
Для
удобства в преобразовании функцию Y
представим в инверсном виде (а в конце
процесса анализа снова вернём в
исходный вид), тогда
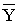 = X4 +
= X4 +
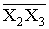 + X1
+ X1
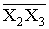 .
.
Используя
закон де Моргана, преобразуем
инверсию конъюнкции
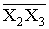 в
дизъюнкцию инверсий т.е.
в
дизъюнкцию инверсий т.е.
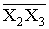 =
=
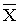 2 +
2 +
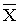 3.
3.
С
учетом правил преобразования функцию
Y приведем к виду
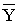 = X4 +
= X4 +
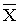 2 +
2 +
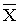 3 + X1 (
3 + X1 (
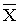 2 +
2 +
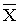 3) = X4 +
3) = X4 +
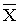 2 +
2 +
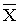 3 +X1
3 +X1
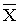 2 + X1
2 + X1
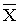 3=
3=
= Х4 +
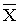 2(1 + X1) +
2(1 + X1) +
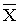 3(1 + X1) = X4 +
3(1 + X1) = X4 +
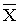 2 +
2 +
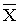 3.
3.
Вернём функцию в исходную форму, т.
е. снова проинвертируем
Y
=
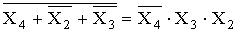 .
.
Полученная функция соответствует
минимальной форме и содержит всего
одну конъюнкцию. Очевидно, в общем
случае может получиться сложное
логическое выражение, требующее
минимизации с использованием
известных методов, в частности карт
Карно.
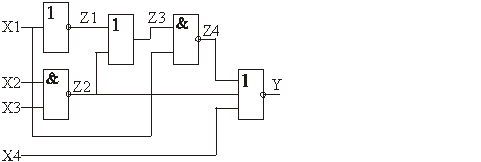
Рис.
2.31 Фрагмент схемы комбинационного
устройства с указанием промежуточных
функций
Схема вновь построенного
комбинационного устройства в базисе
“И-НЕ” приведена на рис. 2.32.
Из
рис. 2.32 следует, что для реализации
операции отрицания переменных Х3
и Х4 использованы элементы “И -
НЕ” с объединенными входами. Такой же
элемент использован для отрицания
промежуточного результата функции
после элемента “3И-НЕ”.
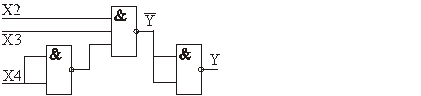
Рис.
2.32. Фрагмент схемы КУ, приведенный в
базис И-НЕ
Схема КУ, приведенная в единый
элементный базис обладает большей
устойчивостью, так как количество
переменных сократилось (в результате
упрощения “выпала” переменная Х1).
|