http://pspicelib.narod.ru

Теоретические основы цепей


ТОЭ1. Цепь переменного тока

       В моё время сделать типовой расчёт по ТОЭ цепи переменного тока было настоящим испытанием терпения. У меня был новый отечественный калькулятор МК-51, и такой счет на первых порах доставлял мне несказанное удовольствие, пока не начали сбоить кнопки. Несолько вечеров было потрачено на глупые перерасчёты. Применение Maple позволяет не заботиться о громоздкости вычислений. Однаков Maplе отсутствует графический интерфейс для ввода электротехнических задач. Этот интерфей можно позаимствовать от какоий либо САПР, например MicroCAP или OrCAD. Тогда ситуация в корне меняется. Тандем MicroCAP-Maple позволяет решить практически любую задачу такого типа в считанные минуты. Причём основное время тратится на рисование схемы.

Рис. 1. Схема  цепи переменного синусоидального тока.

[Maple Bitmap]

>    restart:with(MSpice):ESolve(Q,`01.CKT`);

`Cистема Кирхгофа`

(V5-VOUT)/s/L1+(VIN1-VOUT)/R1+(V3-VOUT)/R2-VOUT*s*C1 = 0

I1-(V3-VOUT)/R2 = 0

(-VIN2-V5)/R3-V5*s*C2-(V5-VOUT)/s/L1 = 0

{VOUT, V5, V3} 

MSpice v8.95:   http://pspicelib.narod.ru

Заданы источники: [VIN2, VIN1, I1]

Заданы узлы: {V4, V2}

Получены решения:

V_NET:=[VOUT, V5, V3]:

J_NET:=[JVIN2, JC1, JC2, JC3, J1, JL1, JR1, JR2, JR3, JVIN1]:

>    VOUT:=simplify(VOUT); JC1:=JC1;

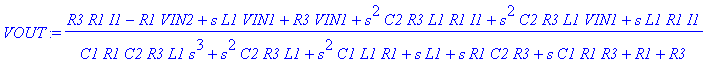
VOUT := (R3*R1*I1-R1*VIN2+s*L1*VIN1+R3*VIN1+s^2*C2*R3*L1*R1*I1+s^2*C2*R3*L1*VIN1+s*L1*R1*I1)/(C1*R1*C2*R3*L1*s^3+s^2*C2*R3*L1+s^2*C1*L1*R1+s*L1+s*R1*C2*R3+s*C1*R1*R3+R1+R3)

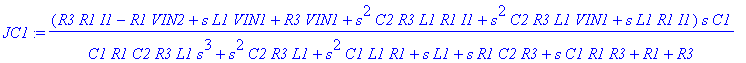
JC1 := (R3*R1*I1-R1*VIN2+s*L1*VIN1+R3*VIN1+s^2*C2*R3*L1*R1*I1+s^2*C2*R3*L1*VIN1+s*L1*R1*I1)/(C1*R1*C2*R3*L1*s^3+s^2*C2*R3*L1+s^2*C1*L1*R1+s*L1+s*R1*C2*R3+s*C1*R1*R3+R1+R3)*s*C1

>    s:=I*2*Pi*f: VOUT:=VOUT; JC1:=JC1;

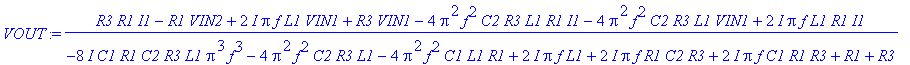
VOUT := (R3*R1*I1-R1*VIN2+2*I*Pi*f*L1*VIN1+R3*VIN1-4*Pi^2*f^2*C2*R3*L1*R1*I1-4*Pi^2*f^2*C2*R3*L1*VIN1+2*I*Pi*f*L1*R1*I1)/(-8*I*C1*R1*C2*R3*L1*Pi^3*f^3-4*Pi^2*f^2*C2*R3*L1-4*Pi^2*f^2*C1*L1*R1+2*I*Pi*f*L...

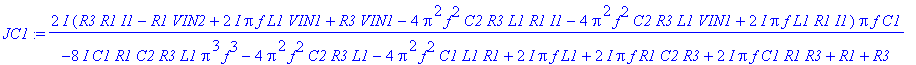
JC1 := 2*I*(R3*R1*I1-R1*VIN2+2*I*Pi*f*L1*VIN1+R3*VIN1-4*Pi^2*f^2*C2*R3*L1*R1*I1-4*Pi^2*f^2*C2*R3*L1*VIN1+2*I*Pi*f*L1*R1*I1)/(-8*I*C1*R1*C2*R3*L1*Pi^3*f^3-4*Pi^2*f^2*C2*R3*L1-4*Pi^2*f^2*C1*L1*R1+2*I*Pi*...

>    Values(AC,RLCVI,[]): 

Номиналы компонентов:   

C1:=10e-9:  [10N]

C2:=0.33e-6:  [0.33U]

C3:=1e-6:  [1U]

L1:=30e-3:  [30M]

R1:=1e3:  [1K]

R2:=330:  [330]

R3:=1e3:  [1K]

AC источник: I1:=0:  AC: I1:=1e-3:   Pfase(degrees):=15:

AC источник: VIN1:=0:  AC: VIN1:=2:   Pfase(degrees):=30:

AC источник: VIN2:=0:  AC: VIN2:=1:   Pfase(degrees):=45:

Источники цепи

>     f:=1e3: I1:=evalf(I1);VIN1:=VIN1;VIN2:=VIN2;

I1 := .9659258263e-3+.2588190451e-3*I

VIN1 := 3^(1/2)+I

VIN2 := 1/2*2^(1/2)+1/2*I*2^(1/2)

Найдем напряжение и ток на выходе OUT

>    VOUT:=evalf(VOUT);VOUT:=evalf(convert(VOUT,polar));
JC1:=evalf(convert(JC1,polar));

VOUT := .3090719852-.8931046018e-1*I

VOUT := polar(.3217170346,-.2813008781)

JC1 := polar(.2021407744e-4,1.289495449)

Переведём фазу сигналов из радиан в градусы

>    Pfase_VOUT:=evalf(convert(argument(VOUT),degrees));
Pfase_JC1:=evalf(convert(argument(JC1),degrees));

Pfase_VOUT := -16.11735308*degrees

Pfase_JC1 := 73.88264690*degrees

ТОЭ2. Цепь переменного тока  

Рис. 1. Схема  цепи. Рабочая частота 1 кГц. Найти амплитуду и фазу напряжения VOUT.

[Maple Bitmap]

>    restart:with(MSpice):ESolve(EQ,`02.CKT`);

`Cистема Кирхгофа`

I2-(V10-V4)/s/L3 = 0

(V8-V9)/s/L2-(V9-V4)/R4 = 0

-(V8-V7)*s*C4-(V8-V9)/s/L2 = 0

I1-(V3-VOUT)/R2 = 0

(VOUT-V4)*s*C1+(V10-V4)/s/L3+(V9-V4)/R4 = 0

(V7-VOUT)/s/L1+(VIN1-VOUT)/R1+(V3-VOUT)/R2-(VOUT-V4)*s*C1 = 0

(V8-V7)*s*C4+(V5-V7)/R3-V7*s*C2-(V7-VOUT)/s/L1 = 0

(-V5+VIN2)*s*C3-(V5-V7)/R3 = 0

-V6*s*C3+(V7-V6-VIN2)/R3 = 0

{VOUT, V10, V3, V4, V5, V6, V7, V8, V9} 

MSpice v8.95:   http://pspicelib.narod.ru

Заданы источники: [VIN1, I2, I1, VIN2]

Заданы узлы: {V2}

Получены решения:

V_NET:=[VOUT, V10, V3, V4, V5, V6, V7, V8, V9]:

J_NET:=[JVIN2, JVIN1, JR2, JR4, JL3, JC2, JR1, JC3, JC1, JC4, J1, J2, JL1, JL2, JR3]:

>    VOUT:=simplify(VOUT):

>    Values(AC,RLCVI,[]):                 s:=I*2*Pi*f: f:=1e3: 

Номиналы компонентов:   

C1:=10e-9:  [10N]

C2:=0.33e-6:  [0.33U]

C3:=1e-6:  [1U]

C4:=1e-6:  [1U]

L1:=30e-3:  [30M]

L2:=10e-3:  [10M]

L3:=10e-3:  [10M]

R1:=1e3:  [1K]

R2:=330:  [330]

R3:=1e3:  [1K]

R4:=1e3:  [1K]

AC источник: I1:=0:  AC: I1:=1e-3:   Pfase(degrees):=60:

AC источник: I2:=0:  AC: I2:=3.4e-3:   Pfase(degrees):=20:

AC источник: VIN1:=0:  AC: VIN1:=2:   Pfase(degrees):=30:

AC источник: VIN2:=0:  AC: VIN2:=1:   Pfase(degrees):=45:

>    print(`Источники сигнала`):
I1:=evalf(I1); I2:=evalf(I2);
VIN1:=VIN1;  VIN2:=VIN2;  IC1:=pIC1;

`Источники сигнала`

I1 := .5000000000e-3+.8660254040e-3*I

I2 := .3194954911e-2+.1162868487e-2*I

VIN1 := 3^(1/2)+I

VIN2 := 1/2*2^(1/2)+1/2*I*2^(1/2)

IC1 := pIC1

>    print(`Выходные сигналы`):
VOUT:=evalf(VOUT); VOUT:=evalf(convert(VOUT,polar));

`Выходные сигналы`

VOUT := 1.866412247-.7433842008*I

VOUT := polar(2.009008399,-.3790363957)

>    print(`Перевод фазы сигнала из радиан в градусы`):
Abs_VOUT:=evalf(abs(VOUT));
Pfase_VOUT:=evalf(convert(argument(VOUT),degrees));

`Перевод фазы сигнала из радиан в градусы`

Abs_VOUT := 2.009008399

Pfase_VOUT := -21.71718575*degrees

ТОЭ3: Работа с комплексными числами в ElectronicsSolver

        Комплексные числа позволяют строить физические модели цепей синусоидального переменного тока. Однако традиционные методы работы с ними хлопотливое дело даже с  таким калькулятором как MathCAD. ESolver решает задачу радикально - ввод комплексных чисел непосредственно в электрическую схему. Это удобно, наглядно и понятно. Решение можно получить для любого узлового  напряжения или тока ветви.

Рис. 1. Схема  цепи переменного тока

[Maple Bitmap]

>    restart:with(MSpice):ESolve(nEQ,`03.CKT`):

`Cистема Кирхгофа`

(VIN1-V1)/Z1+(V4-V1)/Z3 = 0

(VIN2-V4)/Z2-V4/Z4-(V4-V1)/Z3 = 0

{V1, V4} 

MSpice v8.95:   http://pspicelib.narod.ru

Заданы источники: [VIN1, VIN2]

Заданы узлы: {V2, V3}

Получены решения:

V_NET:=[V1, V4]:

J_NET:=[JVIN2, JZ1, JZ2, JZ3, JZ4, JVIN1]:

>    V1:=simplify(V1); V4:=simplify(V4);

V1 := (Z1*Z4*VIN2+Z3*Z2*VIN1+Z3*Z4*VIN1+Z2*Z4*VIN1)/(Z4*Z3+Z2*Z3+Z2*Z4+Z4*Z1+Z2*Z1)

V4 := Z4*(VIN2*Z3+Z1*VIN2+Z2*VIN1)/(Z4*Z3+Z2*Z3+Z2*Z4+Z4*Z1+Z2*Z1)

>    Values(AC,RLCVI,[]): s:=I*2*Pi*f: f:=1000: 

Номиналы компонентов:   

Z1:=(68+I*100):

Z2:=(15-I*56):

Z3:=(-I*80):

Z4:=(-I*634):

AC источник: VIN1:=0:  AC: VIN1:=2:   Pfase(degrees):=30:

AC источник: VIN2:=0:  AC: VIN2:=3:   Pfase(degrees):=45:

>    VIN1:=VIN1; VIN2:=VIN2;
V1:=evalf(V1); V4:=evalf(V4);

VIN1 := 3^(1/2)+I

VIN2 := 3/2*2^(1/2)+3/2*I*2^(1/2)

V1 := .5788331159+1.630584715*I

V4 := 1.444268180+1.714612788*I

>    V1:=evalf(V1); V4:=evalf(V4);

V1 := .5788331159+1.630584715*I

V4 := 1.444268180+1.714612788*I

>    V1:=evalf(convert(V1,polar));V4:=evalf(convert(V4,polar));

V1 := polar(1.730275784,1.229687448)

V4 := polar(2.241831302,.8707725297)

>    Pfase_V1:=evalf(convert(argument(V1),degrees));
Pfase_V4:=evalf(convert(argument(V4),degrees));

Pfase_V1 := 70.45590086*degrees

Pfase_V4 := 49.89159084*degrees

ТОЭ4: Входное сопротивление и входная ёмкость цепи


        Для реального источника сигнала существут максимально допустимое сопртивление и ёмкость нагрузки. По этому, чтобы использовать такой источник, важно знать параметры нагрузки.
       Пусть входной сигнал нагружен на НЧ фильтр (рис. 1). Найти эквивалентное входное сопротивление и входную ёмкость на которую будет нагружен сигнал.
Рабочая частота 1000 Гц.

Рис. 1. Схема  фильтра

[Maple Bitmap]

>    restart: with(MSpice): ESolve(nEQ,`04.CKT`):

`Cистема Кирхгофа`

I1-(V2-V1)/R1 = 0

(V2-V1)/R1-V1/R2-V1*s*C1 = 0

{V1, V2} 

MSpice v8.95:   http://pspicelib.narod.ru

Заданы источники: [I1]

Заданы узлы: {}

Получены решения:

V_NET:=[V1, V2]:

J_NET:=[JC1, J1, JR1, JR2]:

>    Z:=simplify(V2/I1);

Z := (R2+R1+s*C1*R1*R2)/(1+s*C1*R2)

>    Values(AC,RLCVI,[]): s:=I*2*Pi*f: f:=1000: 

Номиналы компонентов:   

C1:=0.68e-6:  [0.68U]

R1:=75e3:  [75K]

R2:=33e3:  [33K]

AC источник: I1:=0:  AC: I1:=1:   Pfase(degrees):=0:

>    Z:=simplify(Z);   Y:=simplify(1/Z);

Z := 75001.65993-234.0396140*I

Y := .1333290842e-4+.4160479571e-7*I

>    eq1:=Im(Y)=2*Pi*f*C: C:=solve(%,C);

C := .6621608894e-11

>    R:=1/Re(Y);

R := 75002.39021

Практически, можно считать, что входное сопротивление на этой частоте чисто активное и равно 75К.

ТОЭ5: Закон Ома

       Графический интерфейс в MicroCAP позволяет весьма удобно и наглядно управлять вводом данных в Maple. В этом примере вместо номинала резистора подставлена формла, где сопротивление резистора выражено через его физические параметры. Однако следует следить за именами переменных и не пересекаться и именами переменных зарезервированными в Maple. Тогда можно воспользоваться функцией unprotect() или выбрать другое имя переменной.

Рис. 1. Схема с резистором  

[Maple Bitmap]

>    restart:with(MSpice):ESolve(MQ,`05.CKT`):

`Cистема Кирхгофа`

I1-V1/R1 = 0

{V1} 

MSpice v8.96:   http://pspicelib.narod.ru

Заданы источники: [I1]

Заданы узлы: {}

Получены решения:

V_NET:=[V1]:

J_NET:=[J1, JR1]:

>    Values(AC,RLC): 

Номиналы компонентов:   

R1:=(4*rho*L/Pi/D^2):

>    R:=simplify(V1/I1);

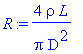
R := 4*rho*L/Pi/D^2

>    unprotect(D):D:=1; V1:=V1, print(`Напряжение`); JR1:=JR1, print(`Ток резистора`);

D := 1

`Напряжение`

V1 := 4*I1*rho*L/Pi

`Ток резистора`

JR1 := I1

ТОЭ6. Цепь переменного тока


Рис. 1. Схема  цепи переменного синусоидального тока.

[Maple Bitmap]

>    restart:with(MSpice):ESolve(Q,`07.CKT`);

`Cистема Кирхгофа`

(V1-V6)/R2+(V7-V6)/R7+(-V6-VE3)/R3 = 0

(V1-V5+VE3)/R2+(V7-V5+VE3)/R7-V5/R3 = 0

-I5+(V1-V7+VE7)/R6+(-V3+VE8)/R8-(V7-V6)/R7 = 0

I5-V2/R4+(V6-V2-VE1)/R2+(V3-V2-VE1)/R6 = 0

-V4/R8-I5+(V1-V4-VE8)/R6+(V6-V3-VE7)/R7 = 0

I5+(-V1+VE1)/R4-(V1-V6)/R2-(V1-V3)/R6 = 0

-I5+(V1-V3)/R6+(-V3+VE8)/R8+(V6-V3-VE7)/R7 = 0

{V2, V1, V3, V4, V5, V7, V6} 

MSpice v8.95:   http://pspicelib.narod.ru

Заданы источники: [VE7, VE3, VE8, I5, VE1]

Заданы узлы: {}

Получены решения:

V_NET:=[V2, V1, V3, V4, V5, V7, V6]:

J_NET:=[JVE8, J5, JR2, JR3, JR4, JR6, JR7, JR8, JVE1, JVE3, JVE7]:

>    V6:=simplify(V6,'size');

V6 := ((((-R8*I5+VE7+VE8)*R6+(VE7+VE8)*R4+R8*(VE1+VE7))*R2+((R7*I5+VE8+VE7)*R4+VE1*(R8+R7))*R6+R7*(R8*VE1+R4*VE8))*R3-(((R8+R7)*R6+(R8+R7)*R4+R8*R7)*R2+((R8+R7)*R6+R8*R7)*R4)*VE3)/(((R6+R8+R4)*R2+(R7+R...
V6 := ((((-R8*I5+VE7+VE8)*R6+(VE7+VE8)*R4+R8*(VE1+VE7))*R2+((R7*I5+VE8+VE7)*R4+VE1*(R8+R7))*R6+R7*(R8*VE1+R4*VE8))*R3-(((R8+R7)*R6+(R8+R7)*R4+R8*R7)*R2+((R8+R7)*R6+R8*R7)*R4)*VE3)/(((R6+R8+R4)*R2+(R7+R...
V6 := ((((-R8*I5+VE7+VE8)*R6+(VE7+VE8)*R4+R8*(VE1+VE7))*R2+((R7*I5+VE8+VE7)*R4+VE1*(R8+R7))*R6+R7*(R8*VE1+R4*VE8))*R3-(((R8+R7)*R6+(R8+R7)*R4+R8*R7)*R2+((R8+R7)*R6+R8*R7)*R4)*VE3)/(((R6+R8+R4)*R2+(R7+R...

>    J[E3]:=simplify(JVE3,'size');

J[E3] := (((-R8*I5+VE7+VE3+VE8)*R2+(R7*I5+VE8+VE7+VE3)*R4+(R8+R7)*(VE1+VE3))*R6+((VE7+VE3+VE8)*R4+R8*(VE7+VE3+VE1))*R2+((VE3+VE8)*R4+R8*(VE1+VE3))*R7)/(((R7+R8+R3)*R2+(R7+R8+R3)*R4+R3*(R8+R7))*R6+((R7+...
J[E3] := (((-R8*I5+VE7+VE3+VE8)*R2+(R7*I5+VE8+VE7+VE3)*R4+(R8+R7)*(VE1+VE3))*R6+((VE7+VE3+VE8)*R4+R8*(VE7+VE3+VE1))*R2+((VE3+VE8)*R4+R8*(VE1+VE3))*R7)/(((R7+R8+R3)*R2+(R7+R8+R3)*R4+R3*(R8+R7))*R6+((R7+...

>    Values(AC,RLCVI,[]): 

Номиналы компонентов:   

R2:=1e3:  [1K]

R3:=1e3:  [1K]

R4:=1e3:  [1K]

R6:=1e3:  [1K]

R7:=1e3:  [1K]

R8:=1e3:  [1K]

AC источник: I5:=0:  AC: I5:=1e-3:   Pfase(degrees):=15:

AC источник: VE1:=0:  AC: VE1:=2:   Pfase(degrees):=30:

AC источник: VE3:=0:  AC: VE3:=2:   Pfase(degrees):=30:

AC источник: VE7:=0:  AC: VE7:=2:   Pfase(degrees):=30:

AC источник: VE8:=0:  AC: VE8:=2:   Pfase(degrees):=30:

Все напряжения и токи цепи

>    V_NET:=evalf(V_NET);

V_NET := [-.6245439474-.4352952387*I, 1.107506861+.5647047613*I, .1915312454+.1852952387*I, -1.540519563-.8147047613*I, 2.165063510+1.250000000*I, 1.923582053+1.185295239*I, .4330127020+.2500000000*I]
V_NET := [-.6245439474-.4352952387*I, 1.107506861+.5647047613*I, .1915312454+.1852952387*I, -1.540519563-.8147047613*I, 2.165063510+1.250000000*I, 1.923582053+1.185295239*I, .4330127020+.2500000000*I]

>    J_NET:=evalf(J_NET);

J_NET := [.1540519563e-2+.8147047613e-3*I, -.9659258263e-3-.2588190451e-3*I, .6744941586e-3+.3147047613e-3*I, .2165063510e-2+.1250000000e-2*I, -.6245439474e-3-.4352952387e-3*I, .9159756152e-3+.37940952...
J_NET := [.1540519563e-2+.8147047613e-3*I, -.9659258263e-3-.2588190451e-3*I, .6744941586e-3+.3147047613e-3*I, .2165063510e-2+.1250000000e-2*I, -.6245439474e-3-.4352952387e-3*I, .9159756152e-3+.37940952...
J_NET := [.1540519563e-2+.8147047613e-3*I, -.9659258263e-3-.2588190451e-3*I, .6744941586e-3+.3147047613e-3*I, .2165063510e-2+.1250000000e-2*I, -.6245439474e-3-.4352952387e-3*I, .9159756152e-3+.37940952...

Hosted by uCoz