Гиратор

        Достоинством гиратора является возможность получать эквивалентные индуктивности на основе активной RС-цепи. Действительно, если в рассматриваемом устройстве по схеме рис. 2 а установить конденсатор С на место Z, то сопротивление Za будет иметь чисто индуктивный характер. Подобные «схемные» индуктивности позволяют строить малогабаритные и высокодобротные LC-фпльтры, предназначенные для работы в области низких частот. При проектировании подобных цепей находит применение достаточно хорошо разработанная классическая теория LC-фнльтров, а при их изготовлении— современная интегральная технология.

Рис. 1. Граф  электронного аналога  переменного конденсатора

Рис. 2. Схема  электронного аналога  переменного конденсатора

>	restart:with(MSpice): Приборы:=[одинаковые,[OP,DC1,3]]: ESolve(Q,`OP-PSpiceFiles/SCHEMATIC1/SCHEMATIC1.net`);

MSpice v8.93:   http://pspicelib.narod.ru

Заданы источники: [Iвх]

Заданы узлы: {}

Получены решения:

V_NET:=[VB, VE, VC, VD, VA]:

J_NET:=[JC, JR2, JR4, Jвх, JR3, JR1]:

Методом вольтметра и амперметра определим входное сопротивление схемы.

>	Zinp:=simplify(VA/Iвх);

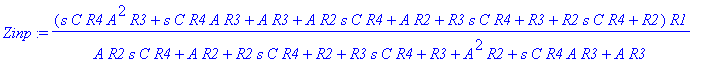
Для упрощения формул примем, что ОУ идеальные и обладают бесконечным усилением.

>	A1:=A: A2:=A:

>	Zinp:=Limit(Zinр,A=infinity)=collect(limit(Zinp,A=infinity),s);

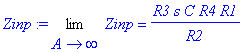
Таким образом, входное сопротивление схемы чистая индуктивность

>	Zinp:=simplify(subs(s=I*omega,rhs(Zinp)));

Пользуясь соотноiением Xc=1/(i*w*C), найдем эквивалентную индуктивность.

>	L:= solve((I*omega*L)=Zinp,L);