Переходные процессы в  нагруженном трансформаторе с ферромагнитным сердечником

.
Анализ переходных процессом методом Лапласа весьма занятное дело. Метод Лапласа хоть и не всесилен, но  необычайно зрелищен  и красив!
Решим этим методом задачу прохождения импульса через трансформатор. На рисунке 2 представлена схема замещения ферритового трансформатора.
В ней учтены потери в обмотках (r1, r2)  и сердечнике (Rm). На вход поступают прямоугольные импульсы. Найти напряжение на нагрузке.

Рис. 1. Схема нагруженного трансформатора с ферритовым сердечником

Рис. 2. Эквивалентная схема для аналитического расчета

>	restart:with(MSpice): with(inttrans): alias(H=Heaviside): ESolve(EQ,`Maqgnetic-PSpiceFiles/SCHEMATIC1/SCHEMATIC1.net`);

MSpice v8.92:   http://pspicelib.narod.ru

Заданы источники: [Vin]

Заданы узлы: {VINP}

Получены решения:

V_NET:=[VOUT, V2, V3, V4]:

J_NET:=[JC2, JVin, JRн, JLm, JC1, Jr1, Jr2, JRm, JLs1, JLs2, JC12]:

>	VOUT:=simplify(VOUT,'size');

>	Values(laplace,RLCVI,[]): Digits:=6: T:=0.008: # Период в сек.

Номиналы компонентов:   

Ls1:=L-M:

Ls2:=L-M:

Rн:=Rн:

Lm:=M:

C1:=C:

r1:=R:

r2:=R:

C12:=Cps:

C2:=C:

Rm:=Rm:

TRANSIENT источник:

Vin:=laplace(-1+2*H(t)-2*H(t-T)+2*H(t-2*T)-2*H(t-3*T)+2*H(t-4*T)-2*H(t-5*T),t,s):

>	Vin:=evalf(Vin);

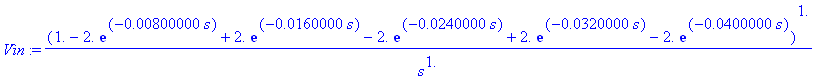
>	L:=500e-3: M:=0.95*L: R:=10: Rн:=100: Rm:=5e3: Cps:=10e-12: C:=50e-12:

>	VOUT:=invlaplace(VOUT,s,t): Vin:=invlaplace(Vin,s,t): Digits:=15:

>	ploth([VOUT,Vin],t=0..4.63e-2,"7) Прохождение импульсов через трансфоматор [VOUT,Vin].");

>	Digits:=2: VOUT:=simplify(VOUT,'size'); # Выходное напряжение