Детектор слабых сигналов

Решение нелинейных схем может доставить удовольствие, если вы сосредоточитесь на главном, а не на составление уравнений Кирхгофа.
До недавнего времени считалось, что такие задачи не имеют явного решения. Однако, не так давно были введены функции Ламберта, и в этих функция оно существует.
В этой схеме диод представлен зависимым источником тока Id=Is*exp((V1-V2)/eta/Vt-1). Применение ОУ позволяет идеализировать характеристики диода. Найдем аналитическое выражение для напряжения на выходе схемы, VOUT=V2.

Рис. 9 . Схема детектора

>	restart:with(MSpice):alias(W=LambertW): ESolve(EQ,`BJT-PSpiceFiles/SCHEMATIC1/SCHEMATIC1.net`):

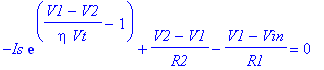
MSpice v8.92:   http://pspicelib.narod.ru

Заданы источники: [Is*exp((V1-V2)/eta/Vt-1), Vin]

Заданы узлы: {VINP}

Получены решения:

V_NET:=[V2, V1]:

J_NET:=[JVin, JRн, JR1, JR2]:

>	VOUT:=simplify(V2,'size');

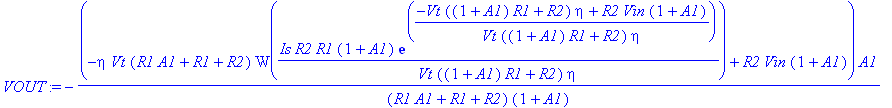
Эта формула упрощается для тех случаев, когда можно считать усиление ОУ бесконечным

>	OUT[A=infinity]:=simplify(limit(VOUT,A1=infinity));

Построим графики выходного напряжения, для номиналов по схеме. Видим, что в нашем случае,  VOUT и OUT совпадают c высокой точностью.

>	Values(DC,RLCVI,[]): omega:=100: eta:=1.8: Vt:=0.025: Is:=1e-8: M:=0.1: Digits:=3:VOUT:=simplify(VOUT);OUT[A=infinity]:=OUT[A=infinity]; ploth([Vin,VOUT,OUT[A=infinity]],t=0..0.2,"9) Входной сигнал и напряжение нагрузки del[Vin,VOUT,OUT(A=infinity)]");

Номиналы компонентов:   

Rн:=2e3:  [2K]

R1:=10e3:  [10k]

R2:=1e6:  [1MEG]

A1:=1e6:  [1e6]

DC источник: Vin:=M*sin(omega*t):