![[Maple Bitmap]](DIFF_1/DIFF_11.gif)
MapleSpice www.pspicelib.narod.ru
Решение ДУ простейшей RC-цепи
С помощью дифференциальных уравнений можно описать любую физическую систему. Если вы это сделаете правильно, то получите математическую модель этой системы, которую можно изучать на экране компьютера. Так например сейчас испытывают ядерные и термоядерные бомбы.
Работа с MSpice хороша тем, что он позволяет сосредоточиться именно на методах решения ДУ, а на не составлении уравнений Киргофа. Уравнения получены, если нарисована схема. Вам остаётся только выбрать метод решения и выставить граничные условия.
Интереснее всего и труднее решать нелинейные задачи, но это единственный путь. К сожалению для нелинейных задач редко удаётся получить решение в явном виде.
Однако ДУ в Maple можно очень точно проинтегрировать численно.
Рис. 1. Схема RC-цепи
![[Maple Bitmap]](DIFF_1/DIFF_11.gif)
| > | restart:with(MSpice):alias(H=Heaviside,delta=Dirac):ESolve(D,`01_RC-цепь/RC1.CKT`): |
![]()
![]()
![]()
![]()
MSpice v8.92: http://pspicelib.narod.ru
Заданы источники: [VIN]
Заданы узлы: {V1}
Решениe: dsolve(ODE union ISc): assign(%);
Решение ДУ
| > | dsolve(ODE union ISc): assign(%); V2(t):=V2(t); |
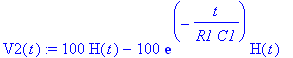
| > | Values(DC,RLC,[]); |
Номиналы компонентов:
C1:=1e-6: [1U]
R1:=10e3: [10K]
| > | ploth([V2(t)],t=0..0.1,"2) График решения ДУ для [V2(t)]"); |
![[Maple Plot]](DIFF_1/DIFF_17.gif)
| > |
MapleSpice
www.pspicelib.narod.ru
Решение дифференциальных уравнений
На вход цепи (рис. 1) поступает синусоидальные сигнал с постоянной составляющей. Найти напряжение на выходе.
Рис. 1. Схема фильтра для блока питания
![[Maple Bitmap]](DIFF_1/DIFF_18.gif)
| > | restart: with(MSpice): ESolve(DDM,`RCL sin/OP-PSpiceFiles/SCHEMATIC1/SCHEMATIC1.net`); |
![]()
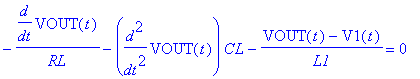
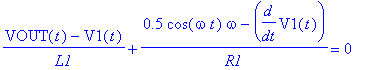
![]()
![]()
MSpice v8.92: http://pspicelib.narod.ru
Заданы источники: [eqVin]
Заданы узлы: {VINP}
Решениe: dsolve(ODE union ISc): assign(%);
| > | dsolve(ODE union {D(VOUT)(0)=0, V1(0)=3.3, VOUT(0)=0}, {VOUT(t),V1(t)}): assign(%); VOUT:=simplify(VOUT(t),'size'); |
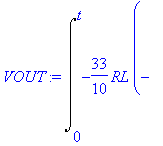
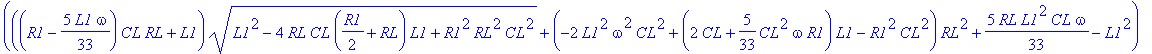
![]()
![]()
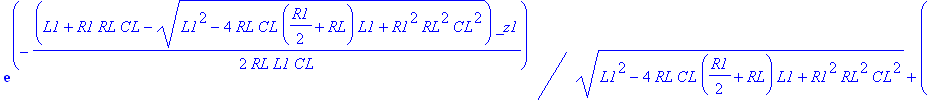
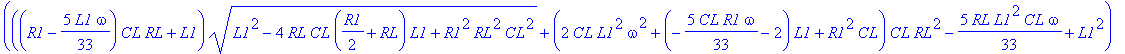
![]()
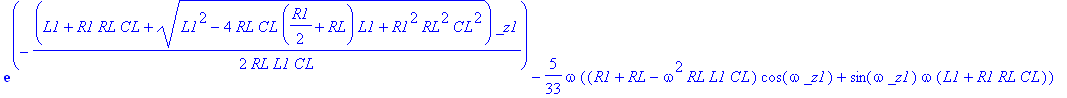
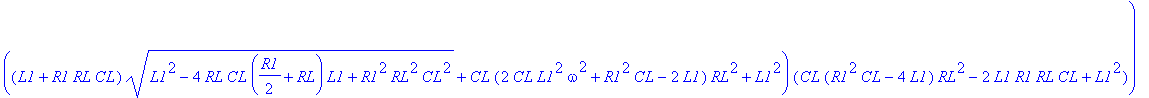
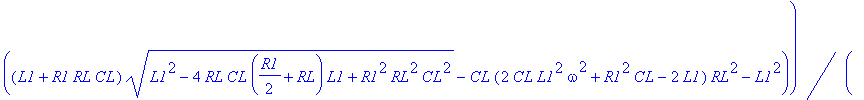
![]()
![]()
![]()
| > | Values(DC,RLCVI,[]); |
Номиналы компонентов:
CL:=200e-6: [200u]
L1:=560e-3: [560mH]
RL:=100: [100]
R1:=10: [10]
| > | Digits:=5: omega:=2*Pi*50: VOUT:=evalf(VOUT); ploth([VOUT,0.5*sin(omega*t)+3.3,0],t=0..0.5,"2) Напряжение на выходе [VOUT(t),0.5*sin(omega*t)+3.3,V0]"); |
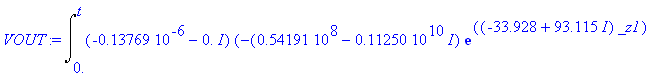
![]()
![[Maple Plot]](DIFF_1/DIFF_129.gif)
MathSpice
http://pspicelib.narod.ru
1. Решение дифференциальных уравнений цепи в MathSpice
Если вы ни разу в жизни не решили дифференциальное уравнение, то MSpice для вас.
MSpice обеспечит вас уравнениями для заинтересовавших вас цепей. А среда Maple хорошо приспособлена для их решения.
Рис. 1. Схема фильтра
![[Maple Bitmap]](DIFF_1/DIFF_130.gif)
| > | restart:with(MSpice): ESolve(DP,`RC1/OP-PSpiceFiles/SCHEMATIC1/SCHEMATIC1.net`); |
![]()
![]()
![]()
![]()
![]()
MSpice v8.92: http://pspicelib.narod.ru
Заданы источники: [eqVin, Eo]
Заданы узлы: {VN6777650}
Решениe: dsolve(ODE union ISc): assign(%);
| > | dsolve({-OUT(t)/RL+(sin(omega*t)+Eo-OUT(t))/R1-diff(OUT(t),t)*C3,OUT(0)=0}):assign(%): OUT:=simplify(OUT(t),'size'); |
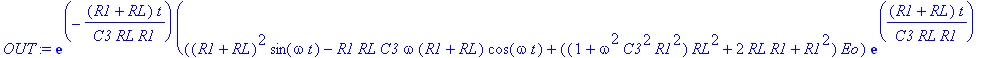
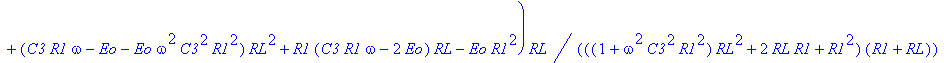
| > | Values(DC,RLCVI,[]); Digits:=5: |
Номиналы компонентов:
C3:=1000e-6: [1000u]
RL:=100: [100]
R1:=10: [10]
DC источник: Eo(t):=3:
| > | Eo:=Eo(t): INP:=sin(omega*t)+Eo; OUT:=OUT; |
![]()

| > | omega:=2*Pi*50; ploth([INP,OUT],t=0..0.21," [INP,VOUT] "); |
![]()
![[Maple Plot]](DIFF_1/DIFF_141.gif)
MathSpice
http://pspicelib.narod.ru
2 . ДУ RLC цепи
На вход цепи (рисю 1) поступает единичный скачёк. Найти напряжение на выходе.
Рис. 1. Схема фильтра
![[Maple Bitmap]](DIFF_1/DIFF_142.gif)
| > | restart: with(MSpice): ESolve(DD,`RCL2/OP-PSpiceFiles/SCHEMATIC1/SCHEMATIC1.net`); |
![]()
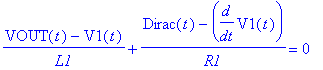
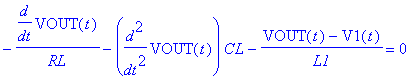
![]()
![]()
MSpice v8.92: http://pspicelib.narod.ru
Заданы источники: [eqVin]
Заданы узлы: {VINP}
Решениe: dsolve(ODE union ISc): assign(%);
| > | Vin(t):=1: |
| > | dsolve(ODE union {D(VOUT)(0)=1, V1(0)=0, VOUT(0)=0}): assign(%); VOUT:=simplify(VOUT(t),'size'); |
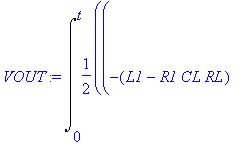
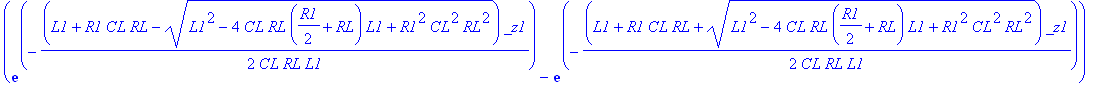
![]()
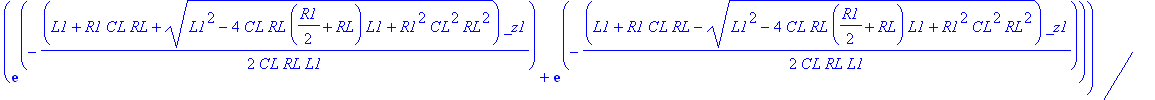
![]()
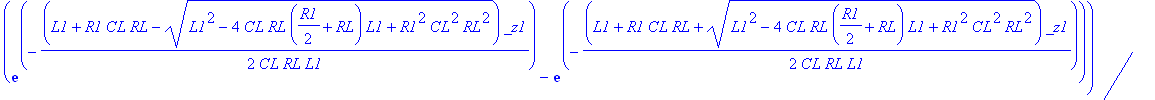
![]()
| > | Values(DC,RLCVI,[]); |
Номиналы компонентов:
CL:=1000e-6: [1000u]
L1:=1: [1H]
RL:=100: [100]
R1:=10: [10]
| > | Digits:=5: VOUT:=VOUT; ploth([VOUT],t=0..0.5,"Рис. 2. [VOUT(t)]"); |
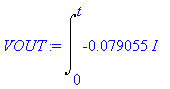
![]()
![[Maple Plot]](DIFF_1/DIFF_157.gif)
3. ДУ последовательного колебательного контура
MathSpice
http://pspicelib.narod.ru
Рассмотрим реакцию последовательно колебательного контура (рис. 1) на воздействие на входе напряжения в виде единичного скачка.
Задачу будем решать методом дифференциальных уравнений.
Рис. 1. Схема последовательного RLC контура
![[Maple Bitmap]](DIFF_1/DIFF_158.gif)
| > | restart: with(MSpice): alias(H=Heaviside,delta=Dirac): ESolve(DD,`RCL1/TX-PSpiceFiles/SCHEMATIC1/SCHEMATIC1.net`); |
![]()
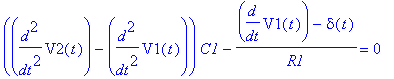
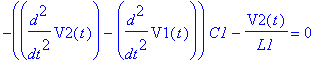
![]()
![]()
MSpice v8.92: http://pspicelib.narod.ru
Заданы источники: [eqVin]
Заданы узлы: {VINP}
Решениe: dsolve(ODE union ISc): assign(%);
| > | dsolve(ODE union {D(V2)(0)=0, V1(0)=0, V2(0)=0}): assign(%): V2:=simplify(V2(t),'size'); |
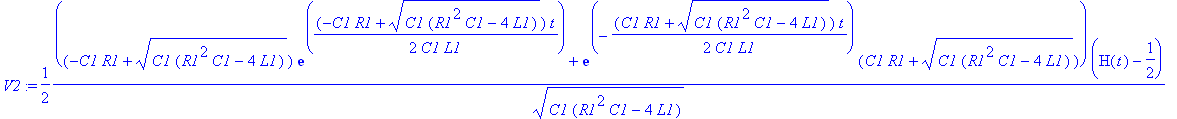
| > | Values(DC); Digital:=15: |
Номиналы компонентов:
C1:=1e-9: [1n]
L1:=1e-3: [1m]
R1:=30: [30]
| > | V2:=simplify(evalf(V2),'size'); ploth([V2],t=0..0.0002,"2) График решения ДУ [V2]"); |
![]()
![]()
![[Maple Plot]](DIFF_1/DIFF_167.gif)
MathSpice
http://pspicelib.narod.ru
4. ДУ фильтра блока питания
Возможность получить решение дифференциальные уравнений цепи очень важно для не линейных задач.
На линейных цепях в большинстве случаев хорошо работает преобразование Лапласа.
Однако если вам требуется получить решение во временной области, то это более короткий путь.
Рис. 1. Схема фильтра
![[Maple Bitmap]](DIFF_1/DIFF_168.gif)
| > | restart: with(MSpice): ESolve(DDP,`RC2/OP-PSpiceFiles/SCHEMATIC1/SCHEMATIC1.net`); |
![]()
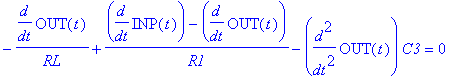
![]()
![]()
![]()
MSpice v8.92: http://pspicelib.narod.ru
Заданы источники: [Eo, eqVin]
Заданы узлы: {VN704687}
Решениe: dsolve(ODE union ISc): assign(%);
| > | dsolve(ODE union {INP(0)=Eo, D(D(OUT))(0)=0, OUT(0)=0}): assign(%); VOUT:=simplify(OUT(t),'size'); |
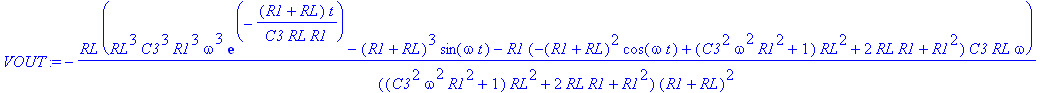
| > | Values(DC,RLCVI,[]);Digits:=5: |
Номиналы компонентов:
C3:=1000e-6: [1000u]
RL:=100: [100]
R1:=10: [10]
DC источник: Eo(t):=3:
| > | Eo:=Eo(t):VINP:=INP(t); VOUT:=simplify(VOUT,'size'); |
![]()
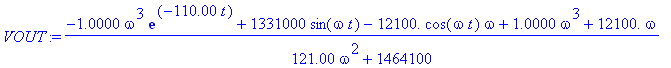
| > | omega:=2*Pi*50; ploth([VINP,VOUT,0],t=0..0.21,"2) Решения ДУ [VINP,VOUT,0]"); |
![]()
![[Maple Plot]](DIFF_1/DIFF_178.gif)
5. Последовательный колебательный контур
MathSpice
http://pspicelib.narod.ru
Рис. 1. Схемат контура
![[Maple Bitmap]](DIFF_1/DIFF_179.gif)
| > | restart:with(MSpice):alias(H=Heaviside,delta=Dirac): ESolve(D,`RCL1/TX-PSpiceFiles/SCHEMATIC1/SCHEMATIC1.net`); |
![]()
![]()
![]()
![]()
![]()
MSpice v8.92: http://pspicelib.narod.ru
Заданы источники: [eqVin]
Заданы узлы: {VINP}
Решениe: dsolve(ODE union ISc): assign(%);
| > | ODE:=diff(ODE,t): for i from 1 by 1 to nops(ODE) do print(eval(ODE[i])): end do; |
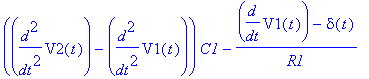
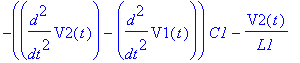
| > | dsolve(ODE union ISc union {D(V2)(0)=0}): assign(%): U2:=simplify(V2(t),'size'); |
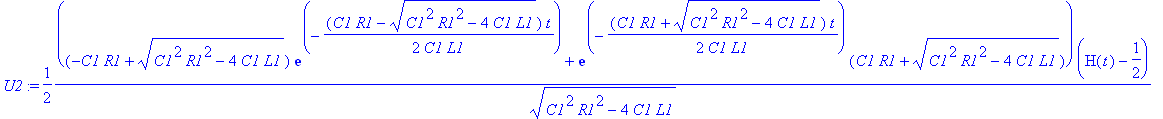
| > | Values(DC,RLCVI,[]); Digital:=12: U2:=simplify(evalc(U2),'size'); |
Номиналы компонентов:
C1:=1e-9: [1n]
L1:=1e-3: [1m]
R1:=30: [30]
![]()
| > | ploth([U2],t=0..0.0002,"TXT"); |
![[Maple Plot]](DIFF_1/DIFF_189.gif)
MapleSpice
www.pspicelib.narod.ru
Дифференциальные уравнения. Конверсия в Mathematica.
Решать практически ценные задачи интересно. Однако при ручном счёте такие задачи быстро утомляют.
Теперь всё по другому. Самым сложным в этой задаче является рисование схемы, а решение получается за секунды.
Рис. 1. Схема усилителя на дифференциальном ОУ
![[Maple Bitmap]](DIFF_1/DIFF_190.gif)
| > | restart:with(MSpice):ESolve(D,`02_RC-цепь/RC1.CKT`): |
![]()
![]()
![]()
![]()
MSpice v8.92: http://pspicelib.narod.ru
Заданы источники: [VIN]
Заданы узлы: {V1}
Решениe: dsolve(ODE union ISc): assign(%);
Преобразуем задача в формат Mathematica
| > | converth([ODE,ISc,"VIN[t]=Sin[300*t]+1;"],mathematica); Values(DC,RLCVI,mathematica): |
ClearAll["Global`*"]; (* MathSpice http://pspicelib.narod.ru *)
VIN[t]=Sin[300*t]+1;
(* Equations of Kirchhoff *)
{V2[t]}/.
DSolve[{-D[V2[t],t]*C1-(V2[t]-HeavisideTheta[t])/R1 == 0,
V2[0]==0}, {V2[t]},t];
{V2[t]}=%[[1]];
VALUE = Simplify[V2[t]]
(* Values of components *)
C1=1*10^-6; [1U];
R1=10*10^3; [10K];
"DC Source"; VIN=1;
(* Numerical calculations *)
INPUT=VINP;
VALUE=Simplify[VALUE] // N
Plot[{INPUT,VALUE},{t, 0, 0.1},Frame->True,PlotStyle->Thick, GridLines->Automatic,PlotRange -> Full]
![[Maple Bitmap]](DIFF_1/DIFF_195.gif)